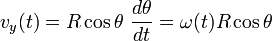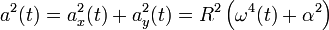Apakah yang terjadi jika benda dikenai gaya?
Pertanyaan ini merupakan pertanyaan yang pernah kita dengar pada pembahasan
fisika sejak kita kelas VII. Bila benda dikenai gaya maka benda akan berubah bentuk, benda
akan bergerak hingga benda akan berubah arah geraknya. Jawaban ini selintas
sangat mudah bagi kita yang sudah duduk di kelas XI.
Dinamika merupakan salah satu bagian dari cabang fisika. Apakah bedanya dinamika dengan
kinematika? Apakah hubungan dinamika dengan mekanika? Untuk lebih jelasnya mari
kita perhatikan contoh dua kasus dibawah ini!
1. Seorang pelari dengan kecepatan awal 10 m/s memiliki percepatan 10 m/s2
2.Suatu benda bermassa 2 kg dikenai gaya sebesar 5 N sehingga benda bergerak dengan
percepatan 0,5 m/s2
Kedua kasus tersebut menggambarkan dua hal yang
sama dan dua hal yang berbeda. Apakah perbedaan dan persamaan kedua kasus tersebut?
Bila kita jeli dalam menganalisa kedua kasus tersebut kita akan mendapatkan
persamaan dan perbedaan dari dua kasus tersebut. Persamaan dari kedua kasus
tersebut adalah sama-sama mengambarkan sesuatu yang bergerak. Apakah perbedaannya? Perbedaan ini merupakan hal yang menarik bagi kita. Perbedaan yang menonjol dari kedua kasus
tersebut adalah kasus pertama menggambarkan benda yang bergerak namun hanya
terfokus pada gerak itu sendiri tanpa memperhatikan faktor yang lainnya. Kasus
kedua merupakan kasus yang lebih sempurna, pada kasus kedua ini selain kita
memperhatikan gerak yang terjadi pada benda namun kita memperhatikan aspek lain
dari gerak diantaranya faktor penyebab gerak berupa gaya maupun faktor benda
itu sendiri misalnya massa benda.
Setelah kita membahas kinematika
partikel pada materi sebelumnya pada bab ini kita membahas mengenai dinamika
partikel yang meliputi segala seluk beluk mengenai gaya. Pada bab ini pembahasan hanya dibatasi pada gaya gesek, gaya gravitasi dan gaya pegas.
Apakah hal yang harus kita persiapkan sebagai
bekal kita dalam mempelajari bab ini? Hal utama yang harus kita persiapkan
adalah pemahaman kita mengenai hukum Newton yang melandasi dinamika partikel.
- Gaya Gesek
membeli sepatu satu bulan yang lalu? Siapakah yang membeli sepatu satu tahun
yang lalu? Atau siapa yang merasa sepatunya sudah tidak baru lagi? Silahkan
memperhatikan permukaan alas sepatu masing-masing! Apakah tebal permukaan alas
sepatu kalian sama ketika baru membeli dengan sekarang? Apakah tingkat
kekasarannya sama antar ketika membeli sepatu dengan sekarang?
Lebih nyaman mana ketika kalian berjalan dengan
sepatu baru dibanding ketika berjalan dengan sepatu yang lebih halus pada
lantai yang lincin? Tingkat kenyamanan
dan keamanan sepatu sebanding dengan tingkat kekasaran sepatu kita terutama ketika
berjalan pada lantai yang lincin. Semakin kasar alas sepatu kita maka semakin
aman ketika berjalan pada lantai yang
lincin. Hal ini disebabkan pada lantai lincin tingkat kerawanan tergelincir
tinggi. Sepatu kasar bisa menurunkan tingkat kerawanan tergelincirnya kaki
kita. Gaya apakah yang menyebabkan kita aman dari tergelincir pada lantai agak
lincin? Apakah yang menyebabkan sepatu kita lebih cepat halus permukaan
alasnya? Gaya ini merupakan gaya gesek yang bekerja dengan arah berlawanan
dengan arah gerak benda dan bekerja ketika benda saling bersentuhan.
1. Gaya gesek statis dan gaya gesek kinetis
Sebelum membahas kedua gaya tersebut sebaiknya
perhatikan demonstrasi berikut!
Gaya Gesek Statis Dan Gaya Gesek Kinetis
Tujuan : 1. Membedakan gaya gesek statis dan gaya gesek kinetis
2. Membedakan koefisisen gesek statis dan koefisien gesek kinetis
Alat dan Bahan : balok kayu, Benang, neraca pegas
Langkah kegiatan:
1. Guru menarik troli dengan menggunakan
neraca pegas yang dikaitkan dengan benang
2. guru menarik troli dari kondisi diam
hingga bergerak dengan gaya yang perlahan-lahan
3. Siswa memperhatikan demonstrasi guru
sambil menulis angka yang tertera pada neraca pegas ketika guru menyebutkan
dengan keras angka yang tertera pada neraca pegas
4. guru membahas mengenai besar gaya yang
diperlukan untuk menarik troli dari diam hingga bergerak
lah memperhatikan demonstrasi ini, kamu akan mengetahui bahwa gaya gesek terdiri
dari gaya gesek statis dan gaya geek kinetis. Gaya gesek statis dan gaya gesek
kinetik memiliki berbagai perbedaan. Bila melihat gaya yang digunakan ketika
kita menarik benda dapat digrafikkan sebagai berikut :
Berdasarkan grafik tersebut terlihat sebelum benda bergerak benda akan mengalami gaya gesek
statis hingga bernilai maksimum hingga tepat akan bergerak. Ketika benda mulai
bergerak, benda mengalami gaya gesek statis.
Perbedaaan apa saja yang terdapat pada kedua gaya gesek tersebut? Perbedaan antara gaya
gesek kinetis dengan gaya gesek statis dapat kita lihat pada kegiatan
demonstrasi kita tersebut. Perbedaaan tersebut antara lain :
| No | Perbedaan | Gaya gesek kinetis | Gaya gesek statis |
| 1 | Kondisi Benda | bergerak | diam |
| 2 | Besar gaya | Relatif konstan | berubah |
| 3 | Komponen yang mempengaruhi | µk dan N | µs dan N |
| 4 | rumusan | Fk = µk.N | Fs ≤ µs.N |
Berdasarkan perbedaan tersebut dapat disimpulkan bahwa gaya
gesek statis bekerja pada benda diam hingga tepat akan bergerak sehingga
besarnya sehingga besarnya gaya
berubah hingga mencapai nilai maksimum yang diperlukan untuk menggerakkan benda.
Jadi jika dirumuskan menjadi Fs ≤ µs.N. Berbeda dengan gaya gesek statis,
gaya gesek kinetis merupakan gaya
gesek yang bekerja pada benda yang bergerak dengan besar gaya yang relatif konstan. Bila dirumuskan
menjadi Fk = µk.N.
Tanda persamaan pada kedua gaya
gesek tersebut memiliki arti fisis yang harus diperhatikan. Apakah arti
fisisnya? Pada gaya gesek kinetis arti tersebut
menandakan besar gaya gesek tersebut relatif konstan dan pada gaya
gesek statis besar gaya
akan terus berubah hingga benda tepat akan bergerak atau bernilai maksimum.
2. gaya gesek pada bidang miring
Bagaimanakah gaya gesek pada
bidang miring? Apakah bidang miring itu? Sebelum membahas lebih jauh tentang gaya gesek pada bidang miring sebaiknya kita melakukan kegiatan berikut.
|
Tujuan : 1. menentukan nilai koefisien gesek kinetis bidang miring
2.menjelaskan pengaruh perubahan sudut terhadap percepatan jatuh benda
Alat dan Bahan: papan lintasan, beban, balok, katrol, mistar, tali,
penyangga, stop watch
Prosedur :
1.Letakkan papan peluncur beserta penyangga dengan sudut tertentu
2.Letakkan balok diatas papan luncur dan ikat dengan tali
3. hubungkan tali dengan beban
4. usahakan tinggi beban terhadap lantai pada sudut berpapun tetap (h) dan massa beban tetap (m)
5. setelah terbentuk sudut kemiringan tertentu
lepaskan beban dari ketinggian tertentu sehingga balok mulai tertarik
mengikuti aarah tali penghubung
6. lakukan langkah ke-5 secara berulang dengan sudut yang berbeda
7. catat sudut pada kolom α, panjang lintasan pada kolom l, waktu yang diperlukan pada





 05.30
05.30
 Rahmad
Rahmad

 Posted in:
Posted in: 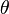 ,
,  dan
dan  atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan
atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan  ,
, 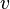 dan
dan  .
.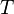


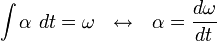
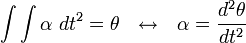

 yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu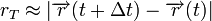
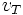 dengan jari-jari lintasan
dengan jari-jari lintasan 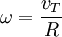
 yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
 , maka dapat pula dituliskan
, maka dapat pula dituliskan

 adalah sudut yang dilalui pada suatu saat
adalah sudut yang dilalui pada suatu saat 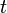 ,
,  adalah sudut mula-mula dan
adalah sudut mula-mula dan  (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial 



 adalah kecepatan sudut mula-mula.
adalah kecepatan sudut mula-mula.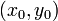

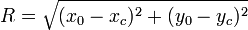


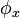 dan
dan 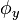 yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai
yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai 

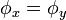





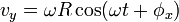
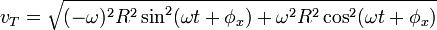

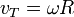



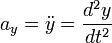
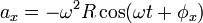







 adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara
adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara